تبادل لینک هوشمند 
نكات مهم ریاضی پایه ششم جهت استفاده دانش آموزان و آموزگاران
|
فصل |
دانلود |
|
اول و دوم |
|
|
سوم |
|
|
چهارم |
|
|
پنجم |
|
|
ششم و هفتم |
|
فعّال بودن دانشآموزان در امر یادگیری، آنان را در مسیری از حرکت و فعّالیّت قرار میدهد. فراگیران در ضمن این فعّالیّت‌ها با مشکلاتی مواجه می‌شوند و ناچار خواهند بود که در جهت رفع این مشکل، کنجکاوانه مراحل پیشرفت کارها را بررسی نمایند و راهحلهای تازه و خلّاقی را تجربه کنند که این امر موجب یادگیری آنان در درس مورد نظر میشود.
مفاهیم ریاضی، یکی از اثر بخشترین و کارآمدترین مواد درسی میباشد. ریچارد کورانت، در این زمینه می‌گوید: «ریاضیات یکی از عالیترین تراوش‌های اندیشهی آدمی است که منعکس کنندهی ارادهی انسان و نشان دهندهی سیر عقلی و میزان علاقهی بشر به کمال و زیبایی است.» نقش بنیادی علم ریاضی در پیشبرد سایر علوم و فنون نیز مورد پذیرش همگان است، به طوری که نرسیدن به اهداف آموزشی درس ریاضی موجب ضعف، ناتوانی و دست نیافتن به اهداف مربوط به پیشرفت علوم و فنون دیگر خواهد بود.[1]
با توجه به مطالب یاد شده، آشکار می‌گردد که نقش و جایگاه درس ریاضی در زندگی انسان دارای اهمیت بسیاری است. اما سؤال این است که، چرا فقط معدودی از معلمان و دبیران در صدد رفع مشکلات ریاضی دانشآموزان هستند؛ در صورتی که نتایج ارزشیابی درس ریاضی اغلب فراگیران رضایت بخش نمی باشد! به راستی چرا اکثر فرهنگیان از انجام پژوهش در این زمینه تردید دارند؟
در همین راستا مولف که خود مدرس دورههای ضمن خدمت درس اقدام پژوهی می باشد، به دنبال پاسخی برای یافتن سوال مورد نظر بود و پس از مصاحبه با بسیاری از فرهنگیان مقاطع مختلف تحصیلی در نواحی چهارگانه استان قم به این نتیجه دست یافت که بسیاری از فرهنگیان به پیشینهی عملی تحقیقات درس ریاضی دسترسی نداشتهاند، بنابر این از انجام پژوهش در این زمینه امتناع میورزند.
بر این اساس، کتاب حاضر مجموعهی اقدام پژوهیهای درس ریاضی فرهنگیان استان قم از دوره اول تا دوره شانزدهم است و هدف آن، علاوه بر آشنایی بیشتر پژوهشگران با پیشینههای عملی تحقیقات درس ریاضی، فراهم آوردن بستری مناسب جهت سهولت دستیابی به راهکارهای اجراشده در این نوع پژوهش نیز میباشد.
با سلام خدمت همکاران خوبم
با توجه به اینکه در ریاضی پایه ششم ابتدایی با کسر ها و اعداد اعشاری و درصد و آمار و احتمال بیشتر سروکار داریم نرم افزاری ساده را برای شما دوست عزیز قرار دادم تا ان شا ا... مفید برای شما باشد و توانسته باشم برای شما معلم زحمت کش خدمتی کرده باشم .
از دانلود این نرم افزار پشیمون نمی شید . فقط نظر یادتون نره
فعالیت ص 52
مقایسه ی دو زاویه با کمک پرگار
دانلودفایل
کار در کلاس و فعالیت ص 57
اندازه گیری زاویه ها ... معرفی متمم ... مکمل
منبع : مجتمع آموزشی نرجس منطقه3
محتوای بسیار زیبای " کارت های متحرک " در قالب فایل فلش برای عزیزان فرهنگی و دانش آموزان گرانقدر تهیه کرده ام ، که امیدوارم در مبحث ضرب و تقسیم اعداد اعشاری کتاب ریاضی پایه ششم ابتدائی ، مفید باشد. این محتوا شامل سه قسمت ضرب و تقسیم اعداد کامل و اعداد اعشاری تا دو رقم و سه رقم می باشد. شما با فشرده دکمه های "+" و یا "-" می توانید عدد مورد نظر را ساخته ، سپس بر روی دکمه های پایینی محتوا کلیک نمائید تا یکی از اعمال ضرب و یا تقسیم بر روی عدد ایجاد شده شما اعمال شود. استفاده از این محتوا در هر سایت و وبلاگی با ذکر منبع بلامانع می باشد .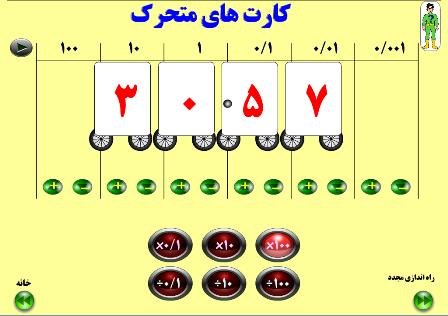
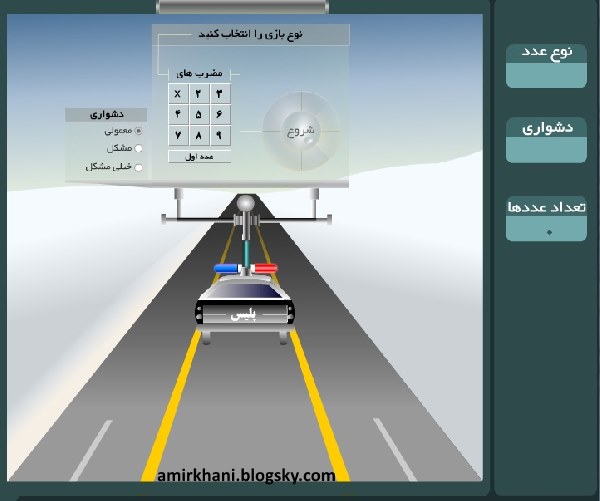
این محتوای الکترونیکی که در قالب یک فایل اجرائی(EXE) ارائه شده و با دوبار کلیک کردن روی آن اجرا می شود ، برای یادگیری هرچه بهتر مضرب های یکی از اعداد 2 و 3 و 4 و ...و 9 بسیار مفید می باشد . از این محتوای آموزشی، معلمان گرامی می توانند برای هیجان و شادی بیشتر در کلاس درس ریاضی و سرگرم کردن دانش آموزان ، استفاده نمایند . دانش آموزان نیز در رایانه های شخصی خود می توانند ، برای یادگیری هرچه بهتر مضرب های اعداد ، همراه با شور و هیجان از این محتوا استفاده نمایند .این محتوای ریاضی دارای درجه دشواری از قبیل : معمولی - مشکل و خیلی مشکل می باشد .برای بازی کردن شما هم از موس و هم از کلید های جهتی صفحه کلید یعنی → و ← استفاده نمائید .
پیدایش رسمی احتمال از قرن هفدهم به عنوان روشی برای محاسبه شانس در بازی های شانسی بوده است. اگرچه ایده های احتمال شانس و تصادفی بودن از تاریخ باستان در رابطه با افسونگری و بخت آزمایی و بازی های شانسی و حتی در تقسیم کار بین راهبان در مراسم مذهبی وجود داشته است و به علاوه شواهدی از به کارگیری این ایده ها در مسایل حقوق، بیمه، پزشکی و نجوم نیز یافت می شود. اما بسیار عجیب است که حتی یونانیان اثری از خود در رابطه با استفاده از تقارنی که در هندسه به کار می برده اند در زمینه احتمال یا اصولی که حاکم بر مسایل شانس باشد بجا نگذاشته اند.
ارسطو پیشامدها را به سه دسته تقسیم می نمود:
1- پیشامدهای قطعی که لزومآ اتفاق می افتادند.
2- پیشامدهای احتمالی که در بیشتر موارد اتفاق می افتادند.
3- پیشامدهای غیر قابل پیش بینی و غیر قابل شناسایی که فقط با شانس محض رخ می دهند.
اما ارسطو به تعبیرهای مختلف احتمال اعتقاد نداشته و فقط احتمال شخصی که مربوط به درجه اعتقاد افراد نسبت به وقوع پیشامدهاست را معتبر می دانسته است.
پاسکال و فرما اولین کسانی هستند که در اوایل قرن هفدهم مسایل مربوط به بازی های شانسی را مورد مطالعه قرار دادند و این دو نفر به عنوان بنیانگذاران تئوری ریاضی احتمال لقب گرفته اند. دانشمندانی از قبیل هی گنز کارهای آن ها را ادامه داده و ویت و هلی این مسایل را در آمارهای اجتماعی به کار گرفتند. این علم جدید نخستین نقطه اوج خود را در اثر مشهوری از ژاکوب برنولی به دست آورد. در این اثر علاوه بر تعریف کلاسیک احتمال ریاضی، اساس خاصی از قانون اعداد بزرگ و کاربردهای احتمال در آمارهای اجتماعی نیز مطرح شده است.
در قرن هجدهم متفکران بزرگی چون دی مور، دانیل برنولی، آلمبرت، اویلر، لاگرانژ، بیز، لاپلاس و گاوس قسمتی از وقت خود را به این علم جدید اختصاص دادند. بیز در سال 1763 قانون معروف بیز را ارایه می دهد و لاپلاس در نوشته ای تمام موضوع علم احتمال را جمع آوری می کند. مهم ترین قضایای حدی که در محاسبات احتمالی به کار می رفته و تاثیر احتمال در ریاضی، فیزیک، علوم طبیعی، آمار، فلسفه و جامعه شناسی در این اثر جمع آوری شده است.
با مرگ لاپلاس در سال 1872 اوج پیشرفت این علم به اتمام رسید و علی رغم برخی تلاش های فردی که ماحصل آن ها کشف قضایایی چون قضیه اعداد بزرگ پواسون و یا نظریه خطاهای گاوس بود، به طور کلی احتمال کلاسیک ارتباط خود را با مسایل تجربی و علمی از دست میدهد. اما جریان های متقابل ظاهر می شوند. به موازات پیشرفت نظریه ریاضی یک نظریه آمار به عنوان کاربردهایی از احتمال به وجود می آید. این نظریه در رابطه با مسایل مهم اجتماعی از قبیل اداره داده های آماری، مطالعه جمعیت و مسایل بیمه به کار می رفته است. اساس کار توسط افرادی چون کوتلت و لکسیز ریخته شده و توسط دانشمندانی چون فشنر(روانشناس)، تیله و برانز(منجمان)، گالتون و پیرسون(زیست شناسان) پیشرفت نموده است. این کارها در اواخر قرن نوزدهم در جریان بوده و در انگلستان و برخی دیگر از کشورها حرفه حسابگری، به مفهوم آماردانی که از اقتصاد و ریاضی هم اطلاعاتی دارد و در جمعیت شناسی و بیمه خبره می شود، رونق می یابد. از طرف دیگر فرمول های کلاسیک ایده های احتمال میز مسیر پیشرفت و کاربردی خود را ادامه می دادند. در این قرن در تلاش برای روشن سازی پایه منطقی کاربردهای احتمال، وان میزز یک فرمول بندی جدید برای محاسبات احتمالی ارایه می دهد که نه تنها از نظر منطقی سازگار بوده بلکه نظریه ریاضی و تجربی پدیده های آماری در علوم فیزیکی و اجتماعی را پایه گذاری می نماید.
مدل کلاسیک احتمال توسط برنولی و لاپلاس معرفی شد. این مدل به دلیل فرض هم ترازی و عدم امکان تکرار در شرایط یکسان و دلایل دیگر با اشکالاتی روبروست که بسیاری از پدیده های طبیعی بر آن منطبق نیست.
ایده های اساسی نظریه تجربی احتمال که قرار دادن فراوانی نسبی به جای احتمال است در سال 1873 توسط پواسون ارایه گردید.
بسیاری از مسایل احتمال حتی قبل از بیان اصول آن توسط کلموگرف در سال 1933 با ابزارهای تجربی و حتی نظری توسط دانشمندان مطرح شده است. ولی کلموگرف با بیان اصول احتمال پایه این علم و ارتباط دقیق آن را با مباحث ریاضی مستحکم می نماید.
در این زمان احتمال به عنوان یکی از شاخه های ریاضی، نه تنها کلیه ابزارهای ریاضی را جهت پیشرفت خود به کار می گیرد، بلکه توانسته کاربردهایی را در حل برخی از مسایل ریاضی داشته باشد. نظریه احتمالی اعداد، نظریه احتمالی ترکیبیاتی و کاربردهای شاخص احتمال در برخی از مسایل آنالیز، بعضی از کاربردهای احتمال در ریاضی هستند.
از طرف دیگر احتمال به عنوان زیربنای ساختاری و اصول ریاضی علم آمار، در جهت پیشرفت این علم و قوام بخشی به دستورات آن نقشی اساسی دارد.
مسایل جالب احتمال هندسی و نظریه احتمالی اعداد، شمه ای از زیبایی های احتمال است که همه اینها با هم زیبایی، کارآیی و توان علم احتمال را نشان می دهند.
صاحب یک گاو، بعد از دوشیدن شیر گاوش، 12 لیتر شیر در یک منبع بزرگ به دست آورده است. او یک ظرف 5 لیتری و یک ظرف 8 لیتری در اختیار دارد و می‌خواهد دقیقاً 6 لیتر از شیر را به ظرف بزرگتر منتقل کند. او چگونه می‌تواند این کار را انجام میدهد؟
جواب در ادامه ي مطالب
ترتیب عملیات :
در عبارتهای که از پرانتز ، ضرب و تقسیم ، جمع و تفریق استفاده شده است ،
ترتیب عملیات در محاسبه ی عبارت عددی به ترتیب زیر است :
الف) کروشه یا پرانتز (حاصل آن را از داخلی ترین پرانتز بدست می آوریم .)
ب) ضرب و تقسیم (از چپ به راست عمل مربوطه را محاسبه کنید)
ج( جمع و تفریق ( از چپ به راست عمل مربوطه را محاسبه کنید )
مثال :
ابتدا عبارت داخل پرانتز را محاسبه کرده، سپس ضرب و تقسیم های مربوطه و در نهایت محاسبه ی جمع و تفریق
نکته ) اگر ترتیب انجام عملیات با پرانتز مشخص نشده بود، ابتدا باید ضرب ها و تقسیم ها ، سپس جمع ها
و تفریق ها را انجام دهید.
مثال : حاصل عبارت مقابل را بدست آورید .
= 11 ÷ (3+(6 - 25)) × 4 + 7
الف) اول کروشه یا پرانتز (حاصل آن را از داخلی ترین پرانتز بدست می آوریم .)
پس اول
19 = 6 - 25
و بعد 22 = 3 + 19
بعد از آن
ب) دوم ضرب و تقسیم (از چپ به راست محاسبه می کنیم)
بنابراین
88 = 22 × 4
و بعد
8 = 11 ÷ 88
و در آخر
15 = 8 + 7
پس جواب برابر 15 می شود .
تو این پست یه روش بسیار آسان و سریع برای محاسبه ی تعداد پاره خط های بالا به شما معرفی می کنم.
روزي علي از دوستش پرسيد : در شكل زير كه از 3 مربع به طول ضلع واحد تشكيل شده است، چند پاره خط مي بيني؟
دوست علي پس از شمارش پاره خط ها ، پاسخ داد: 16 پاره خط .
علي گفت:كاملا" درست است.حال اگر 10 مربع به طول ضلع واحد داشته باشيم،جواب برابر چند است؟
مسلما"دوست علي براي شمارش پاره خط ها به زمان بيش تري نياز داشت.وي چند دقيقه بعد گفت: 121 پاره خط .
علي گفت:درست است .حال اگر 100 مربع به طول ضلع واحد داشته باشيم ،چه طور؟
دوست علي گفت:شمارش پاره خط ها در اين حالت ،كار بسيار دشواري است و از عهده ي من خارج است.
علي گفت :اتفاقا" كار ساده اي است! من رابطه اي به دست آورده ام كه با استفاده از آن به راحتي مي توان تعداد پاره خط ها را براي شكلي كه از
هر تعدادي مربع تشكيل شده باشد به دست آورد.
براي اين منظور كافي است: "تعداد مربع ها را با 1 جمع كرده و حاصل را در خودش ضرب كنيم ."
دوست علي گفت:پس با استفاده از اين رابطه ، تعداد پاره خط ها در مساله ي قبل برابر مي شود.
علي محاسبه ي دوستش را تاييد كرد و هر دو از اين كه يك بحث علمي خوب داشته اند ابراز رضايت كردند.
چندی پیش چینی ها ثابت کردند که:
64 = 65
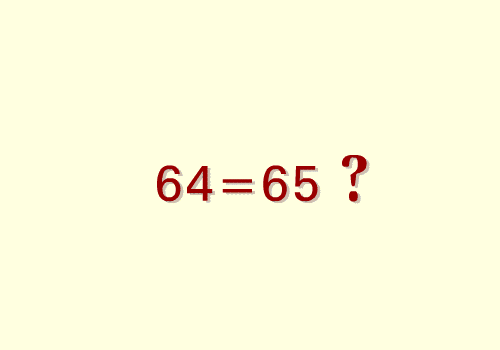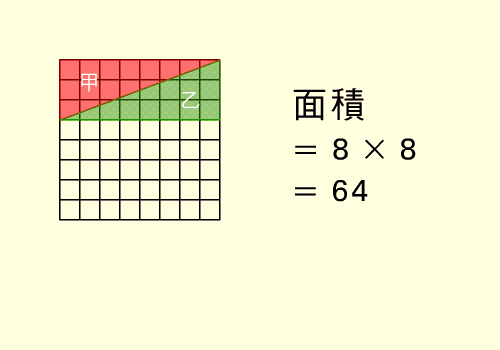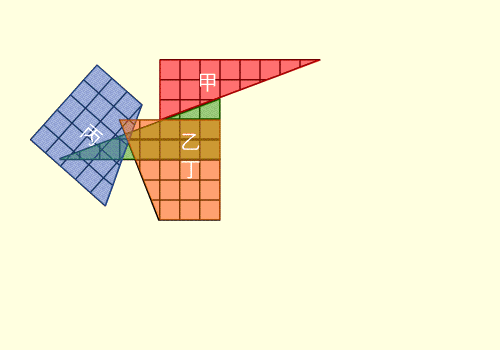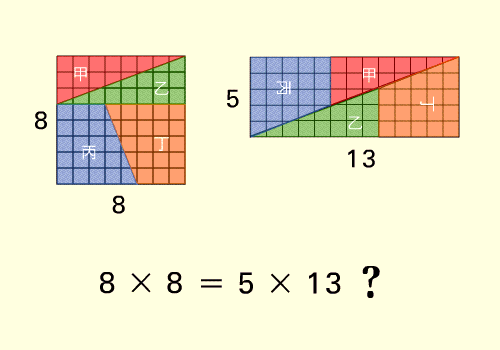
وحالا ما(ایرانی ها) ثابت می کنیم که 25 = 40
این که چیزی نیست و ثابت می کنیم که 25 = 100
روش یادگیری در کلاس
وقتی در کلاس ، جذب سخنان دبیر خود شده‌اید و همه "هوش و حواس" شما متوجه حرف‌های اوست، تقریبا هیچ صدای دیگری را نمی‌شنوید، در حالی که سروصدای کم و بیش یکنواخت بازی بچه‌ها در حیاط مدرسه و یا عبور اتومبیلها در خیابان ، به طور دایم وجود دارد. ولی اگر به سخنان دبیر خود بی‌علاقه باشید، با آن که موج‌های حاصل از صدای او به گوش شما می‌رسد، آنها را نمی‌شنوید. در زبان فارسی ضرب‌المثل جالبی وجود دارد که: "با یک دست نمی‌توان دو هندوانه برداشت". یعنی به طور هم زمان و با هم ، نمی‌توان دو کار را انجام داد. همین اصل روانشناسی است که باید ضمن یادگیری ، مورد توجه قرار گیرد. به چه منظور به مدرسه می‌روید؟ چرا در کلاس درس حاضر می‌شوید؟ مگر نمی‌شود، آن چه را که می‌خواهید و علاقه‌مندید، ضمن مطالعه و پیش خود به دست آورید؟ حقیقت این است که همه چیز را نمی‌توان در کتاب درسی و یا کتاب دیگر پیدا کرد. گذشته از این ، ضمن پرسشهای دانشآموزان و یا بیانهای درست و نادرستی که از زبان دانشآموزان جاری میشود، خیلی چیزها می‌توان آموخت. هنوز عادت نشده است که معلمان و نویسندگان کتابهای درسی یا کمک درسی ، سعی کنند همه تجربه‌های دوران طولانی کار خود را به روی کاغذ بیاورند و در اختیار ما بگذارند. شرکت در کلاس ، روش یادگیری جمعی و راه کار اجتماعی و گروهی را به می‌آموزد. بویژه در زمان ما ، برای پیشرفت دانش نمی‌توان تنها به تلاش‌های فردی متکی بود. در برخورد اندیشه‌ها و در کارهای ویژه‌کاران است که اندیشه‌های نوپدید می‌آید و راه برای عبور از دشواری‌ها باز میشود. اگر عادت کرده‌اید وقتی معلم درس میدهد، با عجله (و به طور طبیعی ، بدون فکر)، همه گفته‌ها و نوشته‌های او را در دفتر خود وارد کنید، باید مطمئن باشید که از درس معلم ، اگر نگویم هیچ بهره‌ای نبرده‌اید، بهره بسیار کمی برده‌اید. کار در منزل قبل از هر چیز تاکید این نکته ضروریست، تکلیفهای مربوط به هر درس را ، در همان روزی انجام دهید که درسش را در مدرسه خوانده‌اید. فرض کنید امروز دوشنبه است و شما درس جبر داشته‌اید. وقتی بعد از پایان کلاسها به منزل می‌رسید، وفتر جبر خود را بردارید و تکلیفهای جبر را انجام دهید. اگر فقط هفته‌ای یکبار و روزهای دوشنبه با دبیر جبر خود روبرو می‌شوید، تکلیف هر هفته را باید عصر دوشنبه همان هفته انجام دهید، نه عصر یکشنبه هفته بعد. شما هر قدر حافظه‌ای نیرومند داشته باشید، با گذشت یک هفته ، بسیاری از نکته‌هایی را که در کلاس شنیده‌اید، از یاد می‌برید و در نتیجه ، نمی‌توانید با موفقیت کامل بر موضوع درس مسلط شوید. بعد از به پایان رساندن کارهای مربوط به همان روز ، کافی است مراجعه‌ای تند به درس‌های فردای آن روز بکنید تا برای فردا آمادگی داشته باشید. برای هر درس یک دفترچه داشته باشید. نوع دفترچه و جنس کاغذ و جلد آن ، حتی تعداد صفحه‌های آن مهم نیست. همه کارهای خود را در همین یک دفترچه انجام دهید. چیزی را پاک نکنید. اگر اشتباهی رخ داد، خط نازکی روی آن بکشید. باید برای خودتان و هم برای دبیرتان روشن باشد، بیشتر در چه زمینه‌هایی اشتباه می‌کنید! تمیزی کار در این نیست که خط خوردگی نداشته باشد، در این است که منظم و خوانا نوشته شود.
پاورپوينت آموزش حجم
آزمون تستی ریاضی ششم 100سوال
همراه با پاسخنامه
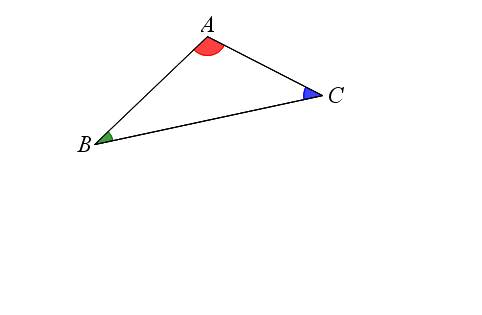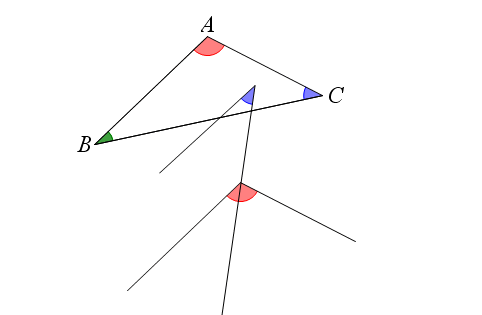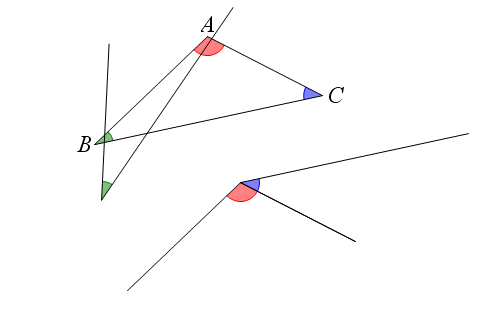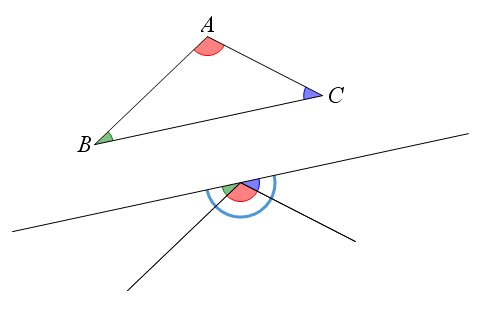
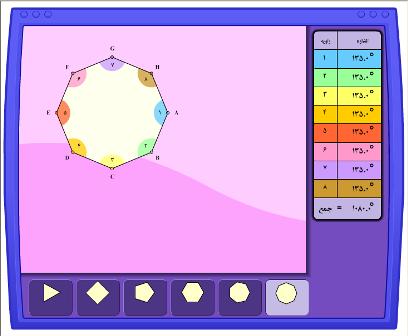
محتوای الکترونیکی مجموع زوایای چند ضلعی
در این محتوا شما با مجموع زوایای چند ضلعی ها آشنا می شوید .حتی با تغییر دادن زوایا هم مجموع آن ها هیچ تغییری نمی کند و ثابت می ماند.این محتوای آموزشی برای مقاطع دبستان و راهنمائی مناسب است.
منبع: www.LRN.ir
قواعد بخش پذیری
برای تقسيم بر بيشتر اعداد طبيعی قاعده هايی وجود دارد. حتی برای برخی از اعداد بيشتر از سه قاعده به دست آمده است که می توان به کمک آن ها بخش پذيری اعداد را بررسی کرد و باقی مانده ه تقسيم آن ها را نيز تعيين نمود. البته در برخی موارد انجام عمل تقسيم، راحت تر از کاربرد قاعده به نظر می رسد. اين به مقسوم و مقسوم عليه بستگی دارد. قاعده تقسيم بر اعداد طبيعی از 1 تا ۱۵ در زير آورده شده است.
قاعده تقسيم بر 1 :
همه ی اعداد بر يک بخش پذير هستند.
قاعده تقسيم بر 2 :
عددي بر 2 بخش پذير است که رقم يکانش بر 2 بخش پذير باشد. باقي مانده تقسيم هرعدد بر 2 باقي مانده تقسيم رقم يکان عدد بر 2 است.
مثال- همه ی اعداد زوج بر 2 بخش پذیر هستند.
قاعده تقسيم بر 3 :
عددي بر 3 بخش پذير است که مجموع ارقامش بر 3 بخش پذير باشد. باقي مانده ی تقسيم عدد بر 3 همان باقي مانده تقسيم مجموع ارقام آن عدد بر 3 است.
مثال- مجموع رقم های عدد 7۵12 برابر 1۵ است و 1۵ بر 3 بخش پذیر می باشد، بنابراین عدد7۵12 بر 3 بخش پذیر است.
قاعده تقسيم بر 4 :
الف) عددي بر 4 قابل قسمت است که دو رقم سمت راست آن بر4 قابل قسمت باشد. باقي مانده تقسيم هر عدد بر 4 مساوي باقي مانده تقسيم دو رقم سمت راست آن عدد بر4 .
مثال- عدد ۵248 بر 4 بخش پذیر است. زیرا 48 بر 4 بخش پذیر است.
ب) عددی بر4 بخش پذیر است که رقم یکان به اضافه ی 2 برابر رقم دهگان آن بر 4 بخش پذیر باشد.
مثال- عدد 1۵68 بر 4 بخش پذیر است. زیرا 20 = 8 + 6 * 2 و 20 بر 4 بخش پذیر می باشد.
قاعده تقسيم بر 5 :
عددي بر۵بخش پذير است که رقم يکانش بر۵ بخش پذير باشد. باقي مانده تقسيم هرعدد بر۵ باقي مانده تقسيم رقم يکان عدد بر ۵ است.
مثال- اعداد ۶۵، 240 و 800 بر۵ بخش پذیر هستند.
قاعده تقسيم بر 6 :
عددی بر 6 بخش پذیر است که بر2 و3 بخش پذیر باشد. ( 3 * 2 = 6)
مثال- عدد 132 هم بر 2 و هم بر 3 بخش پذیراست. پس بر6 نیز بخش پذیر است.
قاعده تقسيم بر 7 :
عددی بر 7 بخش پذیر است که اگر 2 برابر رقم یکان آن را از عددی که از حذف یکان به دست آمده کم کنیم، حاصل بر7 بخش پذیر باشد.(در صورت لزوم این عمل را چندین بار تکرار می کنیم تا به نتیجه برسیم.)
مثال- عدد ۵194 بر 7 بخش پذیر است. زیرا:
49 مضربی از 7 است. بنابراین۵۱۹۴ بر 7 بخش پذیر است.
قاعده تقسيم بر 8 :
الف) عددي بر8 قابل قسمت است که سه رقم سمت راست آن بر 8 قابل قسمت باشد.
مثال- اعداد 4۵000 و706۵6 بر 8 بخش پذیرهستند. زیرا سه رقم سمت راست آن ها یعنی صفر و6۵6 بر 8 بخش پذیرهستند.
ب) عددی بر8 بخش پذیر است که مجموع رقم یکان، به اضافه ی 2 برابررقم دهگان، به اضافه ی 4 برابر رقم صدگان آن بر 8 بخش پذیر باشد.
مثال- عدد ۶۵۳۵۲بر 8 بخش پذیر است. زیرا ۲۴=۲+ ۵* ۲+ ۳* ۴و ۲۴بر ۸بخش پذیر می باشد.
قاعده تقسيم بر 9 :
عددي بر 9 بخش پذيراست که مجموع ارقامش بر9 بخش پذير باشد. باقي مانده تقسيم عدد بر9 همان باقي مانده تقسيم مجموع ارقام آن عدد بر9 است.
مثال- عدد ۵148 بر 9 بخش پذیراست. زیرا مجموع رقم های آن یعنی 18 بر 9 بخش پذیر است.
قاعده تقسيم بر 10 :
عددی بر 10 بخش پذیر است که رقم یکان آن صفر باشد.
مثال- اعداد 70 ، 1200 و 810 بر 10 بخش پذیر هستند.
قاعده تقسيم بر 11 :
عددی بر 11 بخش پذیر است که اگر ارقام آن را یکی در میان به دو دسته تقسیم کنیم و مجموع ارقام هر دسته را به دست آوریم و سپس دو عدد به دست آمده را از هم کم کنیم عدد حاصل بر 11 بخش پذیر باشد.
مثال-عدد ۵240312 بر 11 بخش پذیر است زیرا:
قاعده تقسيم بر 12 :
عددی بر 12 بخش پذیر است که بر 3 و 4 بخش پذیر باشد.
مثال- اعداد 72 و 120 و 480 بر 12 بخش پذیر هستند.
قاعده تقسيم بر 13 :
عددی بر 13 بخش پذیر است که اگر 4 برابر رقم یکان آن را با عددی که از حذف یکان به دست آمده جمع کنیم، حاصل بر 13 بخش پذیرباشد. (در صورت لزوم این عمل را چندین بار تکرار می کنیم تا به نتیجه برسیم.)
مثال- عدد 247 بر 13 بخش پذیر است. زیرا:
قاعده تقسيم بر 14 :
عددی بر 14 بخش پذیر است که بر 2 و 7 بخش پذیر باشد. ( 7 * 2 = 14)
مثال- عدد 3۵42 هم بر 2 وهم بر7 بخش پذیر است. پس بر 14 نیز بخش پذیر است.
قاعده تقسيم بر 15 :
عددی بر 1۵ بخش پذیر است که بر 3 و 5 بخش پذیر باشد. ( ۵ * 3 = 1۵)
مثال- عدد 43۵0 هم بر 3 و هم بر 5 بخش پذیر است. پس بر 43۵0 نیز بخش پذیر است.
منبع : http://ali-nasiri-k.blogfa.com
1 – پاره خط فقط یک نقطه ی وسط دارد .
2 – برای کشیدن یک خط راست کافی است 2 نقطه از آن را داشته باشیم .
3 – نیم خط قسمتی از خط راست است که ابتدای آن مشخص و لی انتهای آن مشخص نباشد . فقط از یک طرف ادامه پیدا کند .
4 – پاره خط قسمتی از خط راست است که ابتدا و انتهای آن مشخص باشد و ما نتوانیم آن را ادامه دهیم .
5 – هر زاویه از دو نیم خط تشکیل شده است .
6 – به نقطه ی مشترک دو نیم خط در زاویه راس زاویه می گویند .
7 – برای خواندن و نوشتن زاویه حرف راس زاویه را در وسط می نویسند .
8 – زاویه به زاویه ی راست یا قائمه ، تند و باز تقسیم می شود .
9 – برای اندازه گیری زاویه ی راست یا قائمه از وسیله ای به نام گونیا استفاده می شود .
10 – زاویه ی تند از زاویه ی راست کوچکتر است .
11 – زاویه ی باز از زاویه ی راست بزرگتر است .
12 – نیم ساز نیم خطی است که از راس زاویه می گذرد و زاویه را به دو قسمت مساوی تقسیم می کند .
13 – دو خط که زاویه ی بین آن ها راست باشد ، دو خط عمود برهم نامیده می شود .
14 – هر مثلثی که یکی از زاویه های آن قائمه باشد مثلث قائم الزاویه نامیده می شود .
15 – به بزرگترین ضلع مثلث قائم الزاویه وتر گویند .
16 – هر چهار ضلعی که فقط دو ضلع موازی داشته باشد ذوزنقه نامیده می شود .
17 – فاصله ی دو خط موازی برابر است با فاصله ی یک نقطه از یک خط تا خط دیگر .
18 – عبارت هایی که درستی تقسیم را نشان می دهد عبارت های تقسیم نامیده می شوند . ( امتحان تقسیم )
19 – در تقسیم همیشه باقی مانده کوچکتر از مقسوم علیه است . این عبارت دوم تقسیم است .
20 – عبارت اول تقسیم ( خارج قسمت ضربدر مقسوم علیه به اضافه ی باقی مانده مساوی است با مقسوم .
21 – واحد اندازه گیری مایعات لیتر است مثل بنزین – نفت .
22 – به مستطیلی که ضلع های آن هم اندازه باشند مربع می گوییم .
23 – به هر لوزی که زاویه های آن قائمه باشند مربع می گوییم .
24 – اندازه ی دور هر شکل محیط آن شکل نامیده می شود .
25 – محیط مربع مساوی است با : اندازه ی یک ضلع ضربدر 4
26 – محیط لوزی برابر است با اندازه ی یک ضلع ضربدر 4
27 – محیط مثلث متساوی الاضلاع برابر است با : اندازه ی یک ضلع ضربدر 3
منبع : ''''وبلاگ آموزگارششم''''
در این روش ضزب به کمک کشیدن خط های افقی و عمودی می توانیم به جواب برسیم
مثال اول :
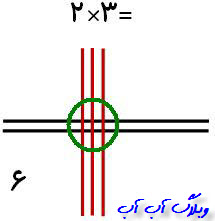
به ضرب نگاه کنید عدد ما 2 است پس 2 خط افقی میکشم
عدد بعدی ما 3 می باشد در نتیجه 3 خط عمودی رسم می کنیم به طوری که خط های موازی را قطع کنن
حالا نقاط تقاطع بدست آمده را شمارش کرده تا حاصل ضرب به دست بیایید
..................................................................................................................................
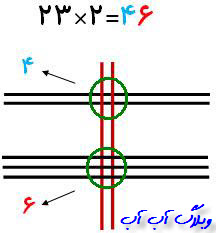
در این ضرب عامل اول از 2 و 3 درست شده است که ما ابتدا 2 خط افقی و سپس با کمی فاصله 3 خط افقی رسم مکنیم حالا نوبت به عامل دوم ضرب یعنی عدد 2 می رسیم که باید 2 خط عمودی رسم کنیم تا از خط های افقی عبور کند
..................................................................................................................................
..................................................................................................................................
..................................................................................................................................
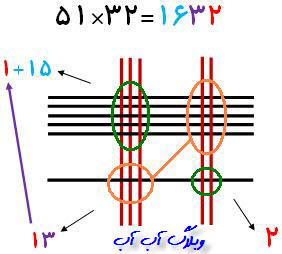
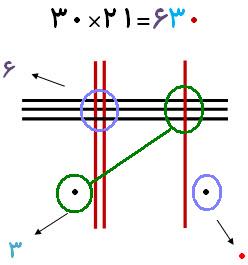
توضیح این روش با جملات بسیار دشوار است بنابراین اجازه بدهید کار خود را با تصاویر شروع کنیم. تصویر زیر را نگاه کنید :
..................................................................................................................................
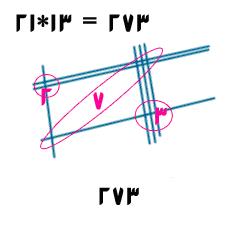
۱- عدد ۲۱ از ۲ و ۱ تشکیل شده پس ابتدا ۲ خط در بالا و ۱ خط در پایین آن به صورت افقی رسم کرده ایم.
۲- عدد ۱۳ از ۱ و ۳ تشکیل شده پس ابتدا ۱ خط و سپس ۳ خط به نحوی رسم کرده ایم که خط هایی که قبلا به صورت افقی رسم کرده بودیم را قطع کنند.
۳- به ترتیب از چپ به راست ابتدا در راس مربع سپس در قطر آن و بعد در راس سمت راست تعداد نقطه هایی که خط ها در آنها یکدیگر را قطع کرده اند را شمرده ایم و ارقام به دست آورده را به همان ترتیب از چپ به راست به عنوان صدگان، دهگان و یکان عدد قرار داده ایم تا به پاسخ برسیم.
..................................................................................................................................
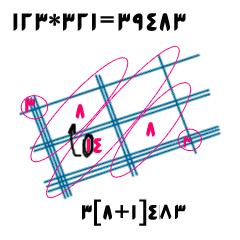
تا اینجا اعدادی که در هم ضرب کردیم دارای ارقام برابر بودند یعنی هر دو سه رقمی یا هر دو دو رقمی بودند. اگر اینطور نباشد چه میشود؟ اجازه بدهید این حالت را هم با یک مثال با هم بررسی کنیم :
..................................................................................................................................
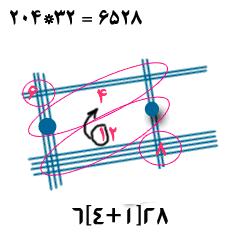
یک مثال دیگر در مورد اعداد صفر دار را با یک دیگر بررسی میکنیم :
..................................................................................................................................
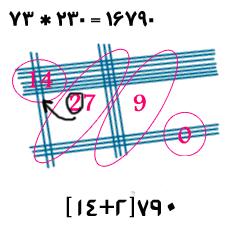
منبع : وبلاگ آب آب
شگفتیهای ریاضیات - علم برای نوجوانان
جهت استفاده از ازمون هاي آنلاين روي لينك زير كليك نماييد
لطفاً نظر فراموش نشود
ازمون جامع برای ششمی ها از درس های هدیه و قرآن و ریاضی و فارسی و علوم و اجتماعی
امیدوارم موفق باشید.
برای دانلود اینجا کلیک کنید. ازمون جامع از تمامی دروس برای شما ششمی ها
امتحان ریاضی ششم ابتدایی (برای محک زدن خودتون)
لطفا حتما بعد از دانلود نظر بگذارید.
دانلود نماييد
آزمون ماهانه ششم(ریاضی،علوم،مطالعات)
تمرین ریاضی ششم دبستان- دانلود كنيد
فاصله ی دو نقطه : فاصله ی دو نقطه طول پاره خطی است که دو نقطه را به هم وصل می کند.(تمرین 3 ص 60 کتاب)
فاصله ی نقطه تا خط : کوتاه ترین فاصله ی یک نقطه تا یک خط ، طول خطی است که از آن نقطه بر خط عمود رسم می شود.(تمرین 4 ص 60 کتاب)
تعریف نیم ساز : نیم ساز خطی است که از راس زاویه می گذرد و زاویه را به دو قسمت مساوی تقسیم می کند.
توجه :فاصله ی هر نقطه روی نیمساز یک زاویه از دو ضلع آن زاویه به یک فاصله است.(تمرین 5 ص 49 کتاب)
بقيه در ادامه ي مطالب
فرمولهای ریاضی مخصوص افرادشرکت کننده در مدارس استعدادهای درخشان
به ادامه ي مطالب مراجعه شود
چرا ریاضى یاد مى‌‌گیریم؟
اساسا، بخاطر سه دلیله: محاسبه، كاربرد، و آخرى، و متاسفانه كمترین از لحاظ زمانى كه به اون اختصاص مى‌‌دیم، الهام بخش بودنه! ریاضى علم الگوهاست، و اون رو مطالعه مى‌‌كنیم تا یاد بگیریم چطور منطقى، منتقدانه و خلاقانه فكر كنیم، اما بخش خیلى زیادى از ریاضى كه تو مدرسه یاد مى‌‌گیریم بطور موثرى انگیزه دهنده نیست، و وقتى هم میپرسیم، “چرا این را یاد مى‌‌گیریم؟” چیزى كه اغلب مى‌‌شنویم اینه كه به زودی میفهمید! یا فوقش اگه دانشجوی فیزیک هم باشید، موقع تدریس درس «ریاضی فیزیک» میگند این توی فلان جای کوانتوم کاربرد داره! خب این اصلا خوب نیست! بهترنیست هر از گاهى ریاضى رو فقط به خاطر این انجام بدیم که جالبه یا زیباست؟ یا به این خاطر كه ذهن را به هیجان میاره؟ بذارید براتون مثالی بزنم از دنباله اعداد دلخواهم، اعداد فیبوناچى!
در ریاضیات سری فیبوناچی به دنباله‌ای از اعداد گفته میشه که غیر از دو عدد اول اعداد بعدی از جمع دو عدد قبلی خود بدست میان. اولین اعداد این سری عبارت‌اند از:
- ۰٬ ۱٬ ۱٬ ۲٬ ۳٬ ۵٬ ۸٬ ۱۳٬ ۲۱٬ ۳۴٬ ۵۵٬ ۸۹٬ ۱۴۴٬ ۲۳۳٬ ۳۷۷٬ ۶۱۰٬ ۹۸۷٬ ۱۵۹۷٬ ۲۵۸۴٬ ۴۱۸۱٬ ۶۷۶۵٬ ۱۰۹۴۶٬ ۱۷۷۱۱
.این اعداد به نام لئوناردو فیبوناتچی ریاضیدان ایتالیایی نام گذاری شده‌است
از نقطه نظر محاسبه، فهمیدنشون آسونه! مثلا یک بعلاوه یک که میشه دو. بعد یک بعلاوه دو که میشه سه، دو بعلاوه سه پنج میشه، سه بعلاوه پنج هم هشت، و الی آخر
از لحاظ کاربرد، اعداد فیبوناچی اغلب در طبیعت به طرزی شگفت آور ظاهر می‌شند. تعداد گلبرگهای یک گل عموما عددی فیبوناچی است، یا تعداد مارپیچ‌های روی یک گل آفتاب‌گردان یا یك آناناس همینطور از قاعده سری فیبوناچی پیروی می‌کنند
ازمون جامع برای ششمی ها از درس های هدیه و قرآن و ریاضی و فارسی و علوم و اجتماعی
امیدوارم موفق باشید.
ازمون جامع از تمامی دروس برای شما ششمی ها
امتحان ریاضی ششم ابتدایی (برای محک زدن خودتون)
لطفا حتما بعد از دانلود نظز بگذارید.
بخش اول ریاضی ششم ابتدای به صورت ورد
بخش اعشار و تقسیم ریاضی ششم ابتدایی ورد
بخش اول جمع و تفریق کسر و مخلوط ریاضی ششم ابتدایی ورد
فرمت ورد
.: Weblog Themes By Pichak :.
آمار
وب سایت:
