عمده ترین روش های حل مساله ریاضی
جستجو برای الگو
رسم شکل
صورت بندی مساله معادل تغییر مساله
انتخاب نمادهای مناسب
استفاده از تقارن
تجزیه به حالت های ساده تر
کار عقب رونده
بررسی نقیض
زوجیت
بررسی حالتهای حدی
تعمیم
عمده ترین روش های حل مساله ریاضی
۱) جستجو برای الگو:
همواره کار حل مساله را با نوعی ادراک شهودی از مساله شروع می کنیم و با بررسی چند حالت خاص به سوی الگوسازی برای حل کامل آن جلو می رویم.
۲) رسم شکل:
در هر مساله ای که امکانپذیر باشد رسم یک شکل (اعم از هندسی یا یک نمودار و غیره) می تواند در یافتن حل مساله الهام بخش باشد و رابطه بین اجزا مساله را بهتر نمایان می سازد.
۳) صورت بندی مساله معادل:
در بخش قبل دیدیم که گام نخست در حل مساله عبارت است از جمع آوری داده - جستجو - فهمیدن مساله - برقراری ارتباط بین اجزا - حدس زدن و تجزیه تحلیل. ولی اگر همه این کارها به روش معقولی میسر نباشد چه کنیم؟ یعنی اینکه ممکن است کارهای محاسباتی خیلی پیچیده باشد و یا به سادگی نتوانیم حالتهای خاصی را مطرح کنیم تا به بینش لازم برسیم.آنچه در چنین شرایطی توصیه می شود این است که مساله را با مساله ای معادل ولی ساده تر جایگزین کنیم. راه کلی در این گونه معادل سازی به بینش و تجربه های عمومی باز می گردد ولی کارهایی از قبیل دستکاریهای جبری یا مثلثاتی و تفسیر مجدد مساله با زبانی دیگر می تواند موثر باشد.
۴) تغییر مساله:
در بعضی مسائل می توانیم مساله مورد نظر را به مساله دیگری تبدیل کنیم. این دو مساله لزوما معادل یکدیگر نیستند ولی حل مساله دوم حل مساله اول را نتیجه می دهد.
۵) انتخاب نمادهای مناسب:
از نخستین گام ها در حل مساله های ریاضی تبدیل مساله به صورتی نمادین می باشد. در انتخاب نمادها باید هر ایده کلی را ملحوظ داشته و آن را با نمادی بیان کنیم. بی دقتی در انتخاب نمادها ممکن است به از بین رفتن یا مبهم شدن بعضی از روابط منجر شود.
۶) استفاده از تقارن:
وجود تقارن در یک مساله موجب می شود که با عملیات کمتری مساله را به جواب برسانیم.
۷) تجزیه به حالت های ساده تر:
گاهی اوقات می توان یک مساله را به تعدادی مساله ساده تر و کوچکتر تبدیل کرد که هر کدام از این مسائل ساده تر را می توان جداگانه در نظر گرفت.
۸) کار عقب رونده:
کار عقب رونده یعنی اینکه نتیجه مورد نظر را مفروض گرفته شروع به استنتاج هایی از آن کنیم تا به یک مساله حل شده برسیم. در این صورت گامهای معکوسی را در نظر بگیریم تا به نتیجه مطلوب دست پیدا کنیم.
۹) بررسی نقیض:
استفاده از تناقض یعنی مفروض گرفتن نادرستی حکم و با استنتاج به نتیجه نادرست یا متناقضی رسیدن از روشهای آشنا در ریاضیات است.
۱۰) زوجیت:
ایده ساده زوج و فرد بودن یکی از ابزارهای بسیار قوی در حل مساله است که کاربردهای وسیعی دارد.
۱۱) بررسی حالت های حدی:
در برخورد اولیه با مساله بعضی اوقات تغییردادن پارامترها بین حدهای پایین و بالای ممکن آنها ایده هایی برای حل مساله به همراه خواهد داشت.
۱۲) تعمیم:
معمولا ساده سازی یک مساله راهگشای حل آن است. اما در بعضی موارد حالت تعمیم یافته مساله سهل تر قابل حل است و حالت مورد نظر را می توان به عنوان یک حالت خاص نتیجه گرفت. در واقع ایده تعمیم و در کنار آن مجرد سازی ویژگی خاص ریاضیات نوین است.
در پایان اشاره می کنم که سعی کنید یک مساله را در صورت امکان به چند روش حل کنید. این کار باعث بهبود سرعت و خلاقیت شما در حل مسائل دیگر می شود. روش های مختلف حل مساله بخش هایی از زوایای پنهان مساله را برای شما آشکار می کند.
آموزش تقریب (قطع كردن و گرد كردن) اعداد با شعر

قطع کردن :
مرتبه رو در بیار زود زیر آن خط بذار
تا اینجا رو نگه دار ادامه اش صفر بذار
به این میگن قطع کردن یاد می گیری تو حتما
گرد کردن :
مرتبه رو در بیار زود زیر آن خط بذار
بعدیش رو، دایره بذار از دایره خبر دار
اگه داره صفر تا چهار ادامه رو صفر بذار
اما بیشتر باشد ز چار روی قبلی یک بذار
ادامش رو صفر بذار گرد همینه، هوشیار
برای دریافت جدول فرآیندی جهت استفاده در جمع و تفریق فرایندی روی نام جدولها کلیک کنید
انیمیشن های آموزشی فصل های سوم و پنجم کتاب ریاضی پایه ششم ابتدایی (اندازه گیری طول و زاویه – نسبت تناسب و درصد) به صورت فایل های فلش را از لینک های زیر دانلود نمایید.
ضمنا برای استفاده از این فایل ها باید نرم افزار فلش پلیر بر روی رایانه شما نصب شده باشد.
| انیمیشن های فصل سوم | |
| انیمیشن های فصل پنجم (فایل های فلش ۱۰ – ۱) | |
| انیمیشن های فصل پنجم (فایل های فلش ۲۰ – ۱۱) | |
| انیمیشن های فصل پنجم (فایل های فلش ۳۰ – ۲۱) | |
| انیمیشن های فصل پنجم (فایل های فلش ۴۰ – ۳۱) | |
| انیمیشن های فصل پنجم (فایل های فلش ۵۰ – ۴۱) | |
| انیمیشن های فصل پنجم (فایل های فلش ۵۸ – ۵۱) |
برای تقسیم یک عدد بر عدد اعشاری مراحل زیر را باید انجام دهیم{مانند شکل پایین}
ابتدا مقسوم و مقسوم علیه را در 10 ، 100 یا 1000 ضرب میکنیم تا مقسوم علیه عددصحیح شود. دو حالت پیش می آید یا مقسوم هنوز عدد اعشاری است یا عدد صحیح درهر صورت دانش آموز ششم دبستان تقسیم عدد اعشاری بر عدد صحیح را میداند ومی تواند این تقسیم را انجام دهد.
در مرحله دوم خارج قسمت را بدون تغییر در تقسیم اول می نویسیم.
در اخرین مرحله باقیمانده را بر عددی که در مقسوم علیه ضرب کردیم
تقسیم می کنیم.

**ریاضی**
نمونه سوال شماره ۱ ریاضی ششم نوبت اول ![]()
نمونه سوال شماره ۲ریاضی ششم نوبت اول ![]()
نمونه سوال شماره ۳ریاضی ششم نوبت اول ![]()
نمونه سوال شماره ۴ریاضی ششم نوبت اول 
نمونه سوال شماره ۵ریاضی ششم نوبت اول ![]()
نمونه سوال شماره ۶ریاضی ششم نوبت اول ![]()
نمونه سوال شماره ۷ریاضی ششم نوبت اول![]()
دانلود مجموعه مسئله های چهارگزینه ای تیزهوشان
دانلود پاسخ نامهسوالات
دانلود نکات ریاضی پایه ی ششم
دانلود نکات فصل1 و 2 دانلود نکات فصل3 دانلود نکات فصل4
دانلود پیک آدینه شماره ۱۴ پایه ششم دبستان
دانلود نمونه تمرین فصل سوم ریاضی ششم، اندازه گیری طول و زاویه
دانلود امتحان فارسی درسهای ۷ و ۸
دانلود نکات مهم فصل ۱ تا ۶ مطالعات اجتماعی پایه ششم
دانلود پیک آدینه شماره ۱۳ پایه ششم دبستان
دانلود آزمون ماهانه ی هدیه آسمان پایه ششم
دانلود نکات درس 6 علوم تجربی پایه ششم (ورزش و نیرو 1)
دانلود نکات فصل 3 ریاضی پایه ششم (اندازهگیری طول و زاویه)
دانلود درس آزاد (درس هشتم) فارسی پایه ششم
دانلود پیک آدینه شماره ۱۲ پایه ششم دبستان
دانلود متن املاء ماهانه از درس ۵ تا ۷ آبان ماه
دانلود تمام چک لیستهای تفکر و پژوهش
دانلود آزمون ماهانه کار و فناوری از درس 1 تا 9
برش و قسمت:
وقتی می خواهیم یک قطعه یا جسمی رشته مانند را به قسمت های مساوی ویا نامساوی تقسیم کنیم همیشه تعداد قسمتها یکی بیشتر از تعداد برشها است.
مثال: یک آهنگر , میله ای به طول 12 متر را به چهار قسمت تقسیم کرد او برای این کار چند برش زده است؟
برش 3 = 1 – 4 (قسمت)
بقيه در ادامه ي مطالب
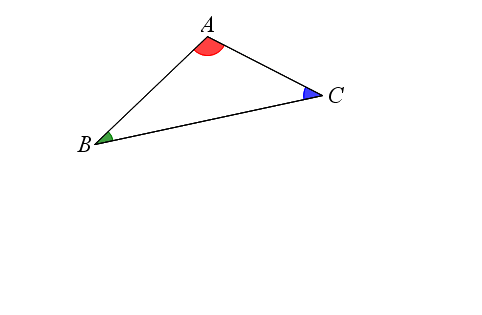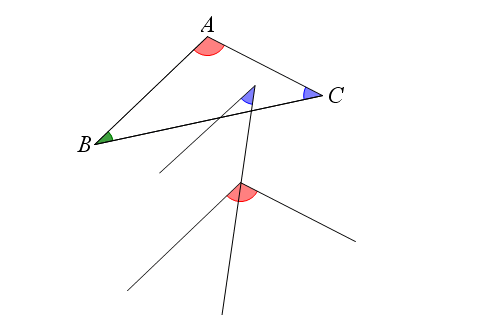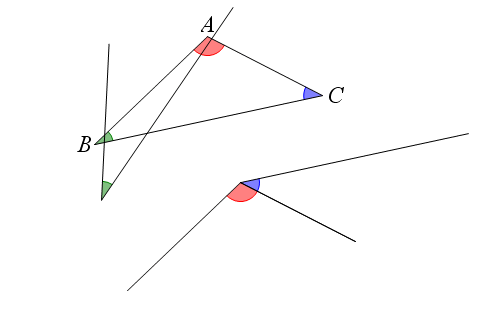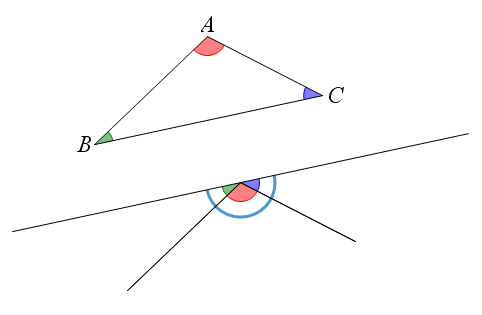
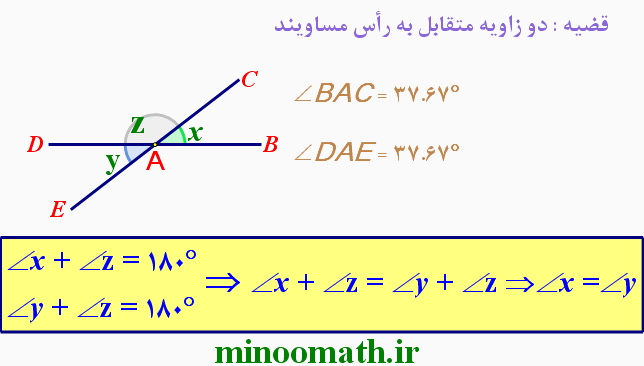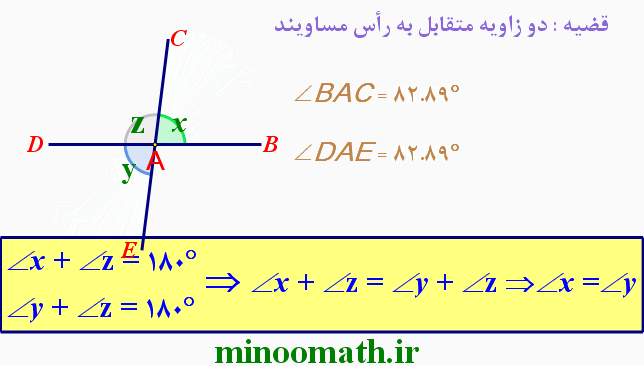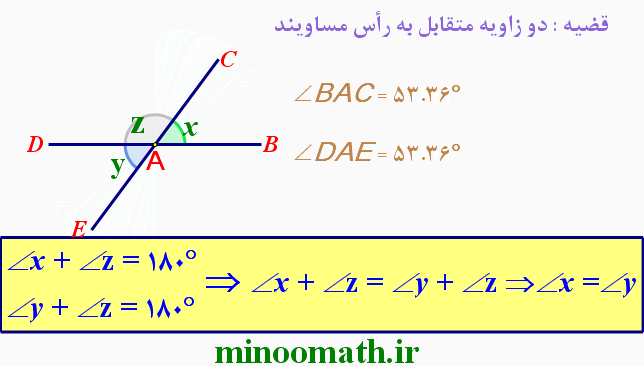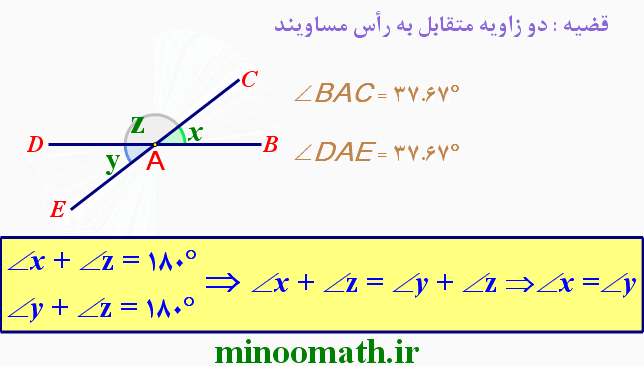
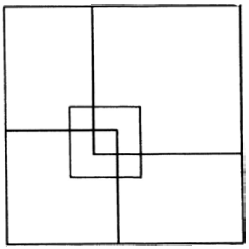
مطابق شکل زیر از رأس های یک مربع به وسط اضلاع آن مربع پاره خط هایی را رسم کرده ایم به طوریکه از برخورد آن ها یک مربع (قسمت رنگی) حاصل شده است.مساحت قسمت رنگی چه کسری از مربع اصلی می باشد؟
جواب را می توانید به صورت انیمیشن در ادامه مطلب ببینید قطعا با دیدن انیمیشن از عهده ی استدلال استنتاجی آن بر می آیید.


در یکی از پست های قبلی (راز های مثلث متساوی الاضلاع ) گفته بودیم که یک مثلث متساوی الاضلاع را می توان به چهار قسمت تقسیم کرد به طوریکه بتوان با آن قطعات یک مربع ساخت اکنون انیمیشنی آماده کرده ام که شما علاقه مندان به ریاضیات می توانید به طور ملموس تری این مساله را ببینید.امیدوارم بپسندید.
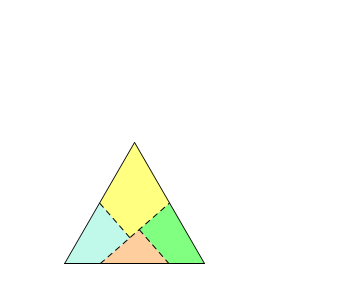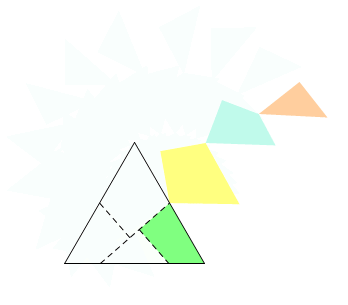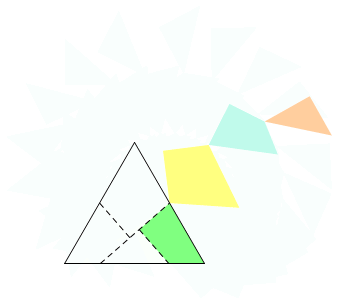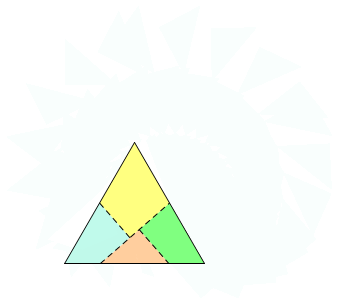
پازل دل کسی رو به هم ریختن هنر نیست...هروقت تونستی با تکه های شکسته ی دل یه نفر یه پازل جدید براش درست کنی هنر کردی!
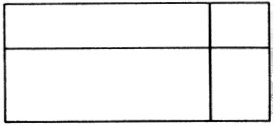
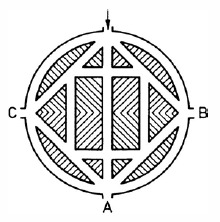
معمای اوّل: در شکل زیر چند مستطیل می توانید ببینید؟

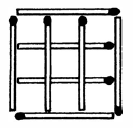
ب) چهار چوب کبریت بردارید به طوری که دو مربع با اندازه برابر باقی بماند.
ج) سه چوب کبریت را حرکت دهید به طوری که سه مربع هم اندازه بسازید.
د) چهار چوب کبریت حرکت دهید به طوری که سه مربع هم اندازه بسازید.
ه) دو چوب کبریت را حرکت دهید به طوری که هفت مربع با اندازه ی متفاوت بسازید.
و) چهار چوب کبریت را حرکت دهید به طوری که ده مربع (نه با اندازه ی یکسان) بسازید.
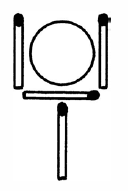
معمای هفتم: همان طور که در شکل زیر می بینید 8 چوب کبریت ، 14 مربع تشکیل داده اند. 2 چوب کبریت بردارید به طوری که فقط 3 مربع باقی بماند.
بقیه معماها را در ادامه مطلب ببینید...

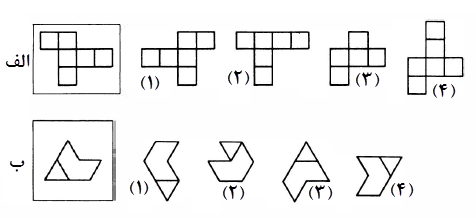
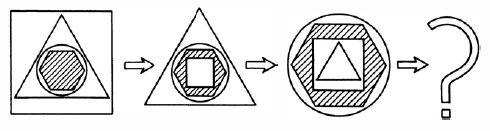
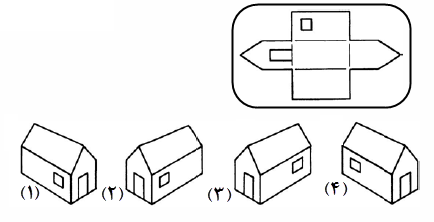


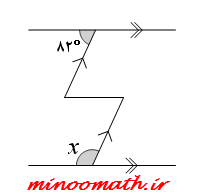
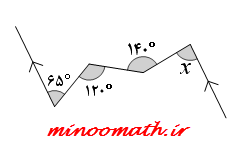
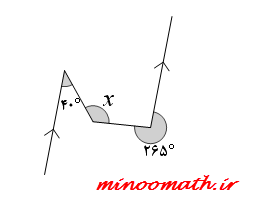
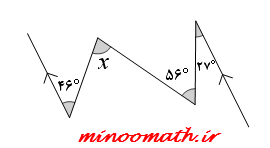
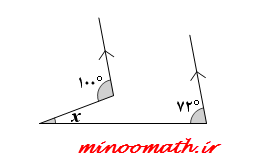
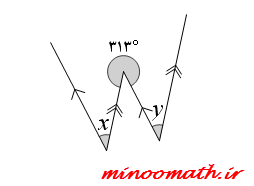
در هر یک از شکل های زیر، اندازه ی زاویه های مجهول x و y را بیابید.(پیکان ها خطوط موازی را نشان می دهند)
انیمیشنی که در زیر به نظر شما گرامیان می رسد در واقع مربوط به مقطع ابتدایی است و بدین صورت دانش آموزان را با مفهوم مساحت دایره آشنا می کنند.ولی توضیح آن برای عزیزانی که مقطع دبیرستان (رشته های ریاضی و تجربی) را گذرانده اند بسیار واضح است.مستحضر هستید که ما در مبحث مساحت و محاسبه آن برای چند ضلعی ها ، مساحت مستطیل را به عنوان اصل می پذیریم و فرمول محاسبه ی مساحت بقیه چند ضلعی ها را بر اساس این اصل اثبات می کنیم.برای بدست آوردن فرمول محاسبه مساحت دایره نیز راضیدان ها ظاهرا از این اصل ایده گرفته اند (گرچه می دانیم که در پایه های بالاتر فرمول مساحت دایره به کمک انتگرال به راحتی بدست می آید) .به هر حال انیمیشن را ببینید و اگر به دلتان نشست ما را از دعای خیرتان بی نصیب نفرمایید. حق یارتان

در هر n ضلعي محدب از هر راس ( n - 3 ) قطر مي گذرد اما چون هر قطر دو بار به حساب مي آيددر نتيجه تعداد قطرهاي n ضلعي محدب برابر است با :
انيميشن زير تعداد قطرهاي n ضلعي محدب تا 12 ضلعي را نمايش مي دهد :


چطور ممکنه ؟؟؟
به نظر شما آیا چنین چیزی وجود حقیقی دارد ؟
.: Weblog Themes By Pichak :.
































































 آمار
وب سایت:
آمار
وب سایت:

